Trigonometría: 5 conceptos básicos que debes conocer
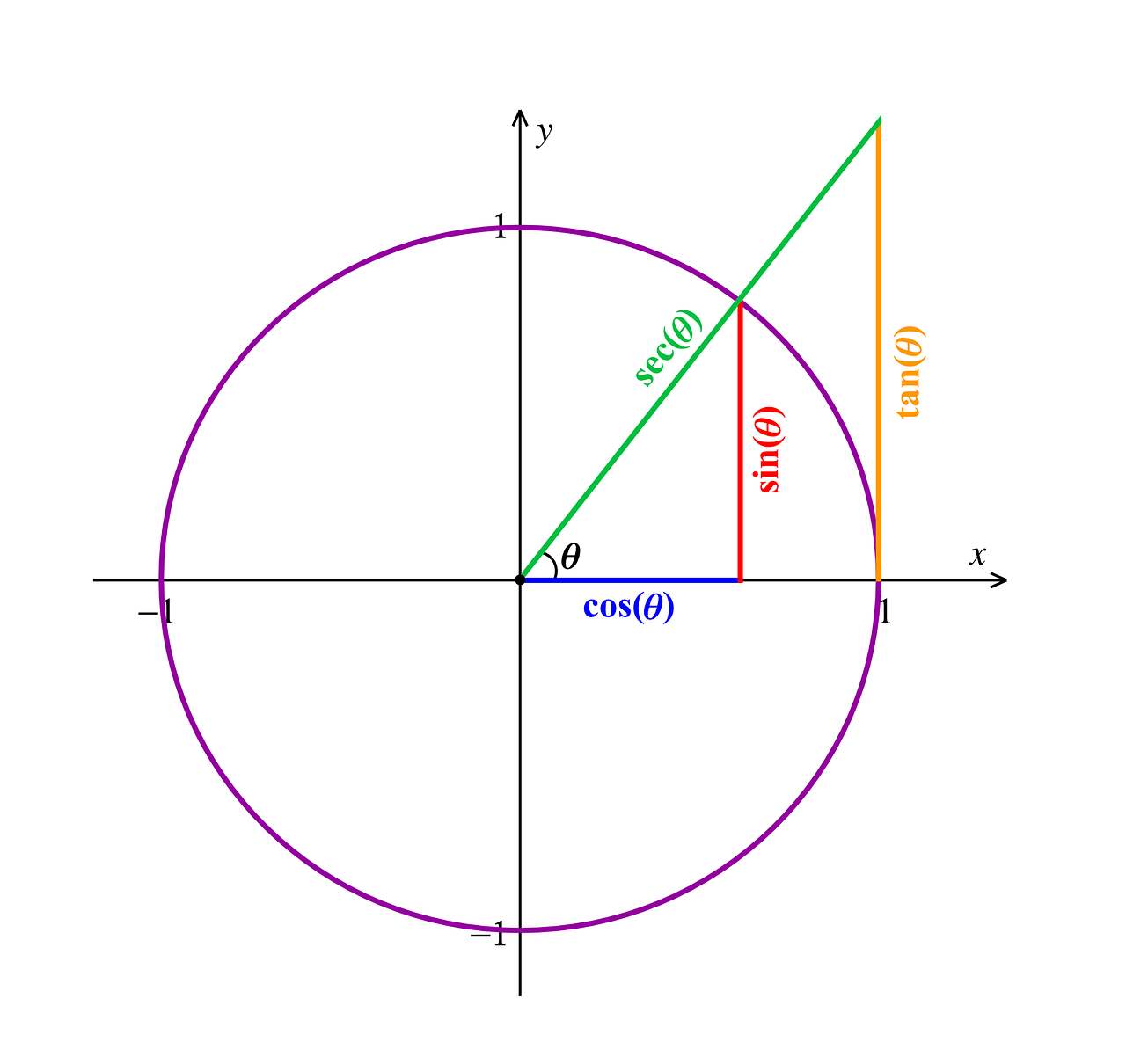
Introducción a la Trigonometría
La trigonometría es una rama de las matemáticas que se enfoca en las relaciones y cálculos angulares de triángulos, con aplicaciones extensas en diversas disciplinas. Desde su origen en la antigua Grecia hasta su uso en la tecnología moderna, la trigonometría ha sido fundamental para comprender las medidas y movimientos en el espacio.
Historia y Evolución de la Trigonometría
Explorar la historia de la trigonometría nos conduce a un viaje fascinante a través de civilizaciones antiguas, donde el estudio de los astros y la geometría desempeñó un papel crucial en el desarrollo de conceptos trigonométricos. Desde las tablas astronómicas babilónicas hasta las fórmulas modernas, la evolución de la trigonometría refleja el ingenio y la curiosidad humanos.
Aplicaciones Prácticas de la Trigonometría
La utilidad de la trigonometría se extiende más allá de los salones de clases, con aplicaciones prácticas en la ingeniería, la arquitectura, la astronomía y la navegación. Comprender los conceptos trigonométricos es esencial para resolver problemas del mundo real, como calcular distancias inaccesibles o diseñar estructuras estables.
Trigonometría en la Tecnología Moderna
En la era de la tecnología, la trigonometría se ha convertido en el fundamento de aplicaciones informáticas, gráficos por computadora, y sistemas de posicionamiento global. La integración de funciones trigonométricas en el desarrollo de software y hardware demuestra su relevancia continua en la innovación tecnológica.
Desafíos y Controversias en la Trigonometría
Los avances en la trigonometría no están exentos de desafíos y controversias, desde la adaptación de métodos tradicionales a la crítica de enfoques educativos. Explorar las posibles limitaciones y debates vigentes en torno a la trigonometría puede enriquecer nuestra comprensión crítica de esta disciplina matemática.
Descubriendo la Trigonometría: Más Allá de los Ángulos y Triángulos
Conceptos Básicos de Trigonometría
La trigonometría es el estudio de las relaciones entre los ángulos y las longitudes de los lados de los triángulos. Desde su origen en la antigua Grecia hasta su relevancia en la actualidad, la trigonometría sigue siendo fundamental en numerosos campos. Al comprender la trigonometría, podemos explorar la manera en que se entrelazan las formas y la geometría con nuestras vidas diarias.
La trigonometría nos permite modelar y comprender fenómenos periódicos, como el movimiento armónico simple, las funciones sinusoidales en electricidad y magnetismo, así como en el análisis de ondas, sonidos y más. Nuestro viaje por los conceptos básicos de la trigonometría nos llevará a explorar las razones trigonométricas y su impacto en nuestro entendimiento del mundo que nos rodea.
Al sumergirnos en este apasionante campo, es crucial tener en cuenta que la trigonometría no se limita a ser simplemente un compendio de fórmulas y cálculos. Más allá de sus aplicaciones matemáticas, la trigonometría nos desafía a pensar en términos de simetría, periodicidad y proporciones, brindándonos una nueva perspectiva para apreciar la belleza matemática en nuestro entorno cotidiano.
Como eslabón crucial en el desarrollo de la matemática y la física, la trigonometría nos invita a explorar las conexiones entre los números, las formas y el movimiento, en un viaje que nos lleva desde los fundamentos de las identidades trigonométricas hasta su relevancia en la resolución de problemas prácticos y teóricos en un amplio espectro de disciplinas académicas y profesionales.
La trigonometría es, en su esencia, una ventana que nos permite vislumbrar la belleza y simetría subyacente en el mundo que nos rodea. Al comprender sus conceptos básicos, nos embarcamos en un viaje fascinante hacia la comprensión de la relación entre las formas, los ángulos y las proporciones, llevándonos a desvelar los misterios ocultos en los movimientos y configuraciones que nos rodean.
Aspectos clave a considerar al estudiar trigonometría:
- Las razones trigonométricas: seno, coseno y tangente.
- La resolución de triángulos mediante leyes y fórmulas trigonométricas.
- Aplicaciones prácticas en la ingeniería, la navegación y la astronomía.
- La interacción de la trigonometría con otras áreas de las matemáticas y la física.
La exploración de la trigonometría nos abre las puertas a una comprensión más profunda de las relaciones matemáticas que yacen en la estructura misma del universo. A medida que nos sumergimos en este fascinante campo, la síntesis entre la teoría y la práctica nos revela la importancia y la belleza que se esconde tras cada ángulo, cada ciclo y cada onda en el mundo que habitamos.
Se anima a los lectores a compartir sus propias experiencias al estudiar trigonometría y a reflexionar sobre el impacto que esta área matemática ha tenido en sus vidas. La trigonometría es mucho más que una colección de fórmulas; es un viaje intelectual que nos lleva a desentrañar los misterios de la estructura y el movimiento en nuestro universo compartido.
¡Explorar la trigonometría es dar un vistazo a cómo los números, las formas y los ángulos se entrelazan para formar el tapiz que constituye nuestro mundo, inspirando asombro y curiosidad a cada paso!
Aplicaciones de la Trigonometría en la Vida Cotidiana
Introducción a la Trigonometría
La trigonometría es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Ya sea resolviendo problemas de medición de distancias, o analizando fenómenos periódicos como las olas del mar, la trigonometría se encuentra en todos lados.
Importancia de la Trigonometría en Navegación
Cuando exploramos un mapa, la trigonometría nos ayuda a calcular distancias, rumbos y posiciones geográficas. Sin esta herramienta, la navegación a través de vastos océanos sería mucho más difícil e incierta. La trigonometría, con sus fórmulas y principios, ha sido crucial para el desarrollo de la navegación marítima a lo largo de la historia.
Trigonometría en la Arquitectura
Los arquitectos y constructores aplican la trigonometría para diseñar y construir estructuras, calculando ángulos, medidas y proporciones para asegurar la estabilidad y funcionalidad. Desde la antigüedad hasta la actualidad, la trigonometría ha sido fundamental en el arte de construir edificios y monumentos.
La Trigonometría en la Música
La trigonometría también se encuentra presente en la música a través de la relación entre las frecuencias de las notas y los patrones de ondas. Compositores y músicos utilizan estos principios matemáticos para crear armonías, escalas, e incluso afinar instrumentos. La intersección entre la trigonometría y la música es fascinante y muestra cómo las matemáticas están integradas en nuestras expresiones artísticas.
La Trigonometría en la Industria Costrucción
Cuando se levantan edificios y se construyen estructuras, la trigonometría es esencial para calcular medidas precisas, ángulos de inclinación y distribución de fuerzas. Desde la planificación inicial hasta la fase de construcción, la trigonometría es una herramienta indispensable para garantizar la seguridad y la durabilidad de las edificaciones.
Exploración Detallada: Aplicaciones de la Trigonometría en la Vida Cotidiana
La trigonometría es una herramienta fundamental en muchos aspectos de nuestras vidas. Desde calcular la altura de un edificio hasta sintonizar un instrumento musical, los principios de la trigonometría están presentes en situaciones cotidianas que tal vez ni siquiera nos detenemos a pensar.
Por ejemplo, al mirar las estructuras arquitectónicas que nos rodean, la influencia de la trigonometría se hace evidente. La inclinación de techos, la colocación de vigas, e incluso la planificación de escaleras, todo se basa en cálculos trigonométricos para garantizar la estabilidad y la seguridad de los edificios.
Además, en el ámbito de la navegación, la trigonometría ha sido crucial para la exploración y el comercio a lo largo de la historia. Desde la antigüedad, los navegantes han confiado en los principios trigonométricos para trazar rutas, calcular distancias y mantenerse orientados en alta mar.
En resumen, la trigonometría no es solo una abstracción matemática, sino una herramienta práctica que impacta nuestras vidas diariamente de maneras sorprendentes e imperceptibles.
Para obtener más información sobre trigonometría, puedes consultar el artículo de Wikipedia.
Para ampliar tus conocimientos sobre el uso de la ley de senos en trigonometría, te recomiendo visitar el artículo de Wikipedia.
Si estás interesado en aprender más sobre la trigonometría esférica, te invito a explorar el artículo de Wikipedia.
Ejemplos Prácticos de Trigonometría
Descubriendo el Mundo de la Trigonometría
Introducción a la Trigonometría
La trigonometría es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. No es solo una herramienta teórica, sino que tiene aplicaciones prácticas en diversas áreas, desde la navegación hasta la ingeniería.
Importancia de la Trigonometría en la Vida Diaria
Cuando planificas un viaje por carretera y necesitas calcular distancias y ángulos, estás utilizando conceptos trigonométricos. La trigonometría también se encuentra presente en la arquitectura, la física y la astronomía. ¿Quién diría que la trigonometría es tan relevante en nuestro día a día?
Aplicaciones Innovadoras de la Trigonometría
En la actualidad, la trigonometría se utiliza en campos tan diversos como la animación por computadora, el diseño de videojuegos y la cartografía digital. Su influencia es fundamental en la creación de mundos virtuales y gráficos avanzados.
Eficiencia en la Enseñanza de la Trigonometría
¿Cómo podemos hacer que el estudio de la trigonometría sea más atractivo para las nuevas generaciones? Quizás la clave esté en la creación de recursos interactivos y en la contextualización de los conceptos, permitiendo a los estudiantes comprender su utilidad práctica.
Descubriendo la Belleza de los Triángulos
La trigonometría nos presenta patrones sorprendentes en las relaciones entre los ángulos y los lados de los triángulos. Estos descubrimientos matemáticos han fascinado a generaciones, y continúan siendo un área de estudio apasionante.
Profundizando en la Trigonometría Aplicada
Al explorar las aplicaciones de la trigonometría, podemos descubrir un mundo de posibilidades. Desde el diseño de estructuras arquitectónicas hasta la creación de efectos visuales en el cine, la trigonometría impulsa la innovación en la ciencia y la tecnología.
- La trigonometría en la medicina: analizando ángulos articulares para diagnósticos precisos.
- Aplicaciones de la trigonometría en la ingeniería civil y la construcción de infraestructuras.
- Explorando la relación entre la trigonometría y la música, revelando patrones armónicos.
La trigonometría es mucho más que teoremas y cálculos; es una herramienta para comprender y modelar el mundo que nos rodea de manera sorprendente.
Recursos Adicionales sobre Trigonometría
Explorando el Mundo de la Trigonometría
¿Qué es la Trigonometría?
La trigonometría es una rama de las matemáticas que se enfoca en las relaciones y cálculos relacionados con triángulos y funciones angulares. Desde la antigüedad, ha sido fundamental en la navegación, la astronomía y en la resolución de problemas geométricos. La trigonometría nos permite comprender la relación entre los ángulos y las longitudes de los lados de un triángulo. Además, a menudo se aplica en contextos del mundo real, como la arquitectura y la ingeniería. Exploraremos sus conceptos fundamentales y su aplicación práctica en esta narrativa.
Aplicaciones de la Trigonometría en la Vida Cotidiana
La trigonometría no solo reside en los libros de texto, sino que se manifiesta en numerosas situaciones diarias sin que nos demos cuenta. Por ejemplo, al lanzar una pelota de fútbol, el cálculo mental para ajustar la trayectoria involucra conceptos trigonométricos, aunque de manera inconsciente. ¿Quién hubiera pensado que la trigonometría está presente en nuestras actividades recreativas más simples? Exploraremos estos escenarios cotidianos donde la trigonometría despliega su magia, a menudo inadvertida por muchos.
Descubriendo los Secretos de la Trigonometría
La trigonometría se abre camino en nuestro día a día de formas sorprendentes. Desde el diseño de videojuegos hasta el cálculo de trayectorias de cohetes espaciales, su influencia es omnipresente. Incluso en el arte y la música, los patrones trigonométricos se entrelazan en composiciones visuales y sonoras. A través de la trigonometría, podemos explorar la belleza matemática que subyace en las creaciones humanas más aparentemente desligadas de las matemáticas.
La Trigonometría en la Era Digital
En el mundo digital actual, la trigonometría se manifiesta de maneras inesperadas. Desde la renderización de gráficos en videojuegos hasta la compresión de datos en la transmisión de medios, este campo matemático impulsa numerosos aspectos de la tecnología moderna. Exploraremos cómo la trigonometría se integra en la era digital y su papel en el desarrollo de avances tecnológicos que han transformado nuestra sociedad.
El Futuro de la Trigonometría
Adentrarse en los avances actuales y futuros de la trigonometría revelará cómo esta disciplina sigue evolucionando y adaptándose a las demandas de un mundo en constante cambio. Desde la programación de inteligencia artificial hasta la exploración espacial, la trigonometría continuará desempeñando un papel vital en la resolución de problemas complejos que desafían los límites de nuestra comprensión. Un vistazo a las proyecciones futuras de la trigonometría nos permitirá vislumbrar su papel en la vanguardia del conocimiento y la innovación.
Recursos Adicionales sobre Trigonometría
- El uso de la trigonometría en la era espacial
- Las aplicaciones de la trigonometría en el diseño de videojuegos
- Trigonometría y la música: una conexión inesperada
¡Explora estos fascinantes enlaces para descubrir más sobre la trigonometría y su relevancia en diversos ámbitos!
Clic aquí para obtener más información sobre trigonometría en Wikipedia
Para descubrir más sobre los términos relacionados con la trigonometría, revisa los siguientes enlaces: Funciones trigonométricas, Teorema de Pitágoras, Triángulo rectángulo.
La importancia de la trigonometría en las matemáticas: conceptos fundamentales y aplicaciones.
La trigonometría es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de un triángulo. Es fundamental en matemáticas por su amplio rango de aplicaciones en diversas áreas como la física, la ingeniería, la astronomía y la navegación.
Uno de los conceptos fundamentales en trigonometría es el teorema de Pitágoras, que establece la relación entre los lados de un triángulo rectángulo. Otro concepto clave es el teorema del seno y del coseno, que permiten calcular longitudes y ángulos en triángulos no necesariamente rectángulos.
En cuanto a sus aplicaciones, la trigonometría se utiliza para resolver problemas relacionados con medidas angulares, distancias inaccesibles, movimientos periódicos, análisis de ondas y muchas otras situaciones cotidianas. Es una herramienta poderosa para modelar fenómenos naturales y resolver problemas prácticos en diversas disciplinas científicas.
En resumen, la trigonometría es una disciplina matemática fundamental con múltiples aplicaciones prácticas en diferentes campos del conocimiento. Su comprensión es crucial para abordar problemas complejos y avanzar en el desarrollo científico y tecnológico.
Razones TRIGONOMÉTRICAS de Cualquier Ángulo 🔵 con Circunferencia GONIOMÉTRICA
[arve url=»https://www.youtube.com/embed/bTCc8fQl-s0″/]RAZONES Trigonométricas 0, 90, 180, 270 y 360 🔵 CIRCUNFERENCIA Goniométrica
[arve url=»https://www.youtube.com/embed/CnRfsJSeXmM»/]ASÍ se GRAFICAN SEN y COS▶ DOMINIO y RANGO DE LAS FUNCIONES TRIGONOMÉTRICAS SEN Y COS 📐📖
[arve url=»https://www.youtube.com/embed/LMkc5QNp7k4″/]Preguntas Frecuentes
¿Qué es la trigonometría?
La trigonometría es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos.
¿Cuáles son las principales funciones trigonométricas?
Las principales funciones trigonométricas son seno, coseno y tangente.
¿Cómo se utilizan las identidades trigonométricas en problemas matemáticos?
Las identidades trigonométricas se utilizan para simplificar expresiones trigonométricas y resolver ecuaciones relacionadas con ángulos y triángulos en problemas matemáticos.
¿Cuál es la relación entre la trigonometría y la geometría?
La trigonometría es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de un triángulo. La geometría, por otro lado, se encarga de estudiar las propiedades y medidas de figuras en el espacio. La relación entre ambas disciplinas radica en que la trigonometría se utiliza para resolver problemas geométricos que involucran triángulos, ayudando a calcular longitudes, áreas y ángulos en diferentes figuras geométricas.
¿En qué situaciones cotidianas se aplica la trigonometría?
En el contexto de la vida diaria, la trigonometría se aplica en situaciones como la navegación marítima, la construcción de edificios, el diseño de videojuegos y en problemas relacionados con la geometría espacial.
En conclusión, la trigonometría es una rama fundamental de las matemáticas que estudia las relaciones entre los ángulos y los lados de un triángulo. A través de sus funciones trigonométricas como el seno, coseno y tangente, podemos resolver problemas geométricos y aplicarlos en diversas áreas de la ciencia y la tecnología. ¡Explora el fascinante mundo de la trigonometría y descubre sus infinitas aplicaciones! ¡No temas a los triángulos, abraza la trigonometría!

